Introduction

Great progress has been achieved in building quantum information processing (QIP) devices, such as by using superconducting circuits1,2,3. Although superconducting circuits have many advantages such as simple configurability, and up to 53 superconducting qubits have been fabricated and connected1, they have a short decoherence time and need to be kept at a very low temperature. Currently, most QIP devices indispensably rely on the control of ultralow temperatures down to millikelvin2. Hence, quantum gate operations at higher temperatures are still an inevitable obstacle to overcome for a practical QIP device4. Optical excitations, especially in organic materials, could be one of the solutions, offering larger energy scales for coherent interactions against incoherent thermal noise due to the high temperature (~77 K, the boiling point of liquid nitrogen)5,6,7. By using optical excitations, we can also avoid the decoherence induced by the external electrodes conventionally used for the control of electrons8. Moreover, the spins in organic molecules can have a long spin-lattice relaxation time (T1) due to the weak hyperfine interaction and spin-orbit coupling9 and a long spin-spin relaxation time (T2, characterizing the transverse relaxation process owing to spin-spin interactions) because of the controllably weak coupling between spins. For example, the T1 time for diluted copper-phthalocyanine (CuPc) can reach microseconds at 200 K10. In the meantime, the T2 time for diluted CuPc, which is very important for fault-tolerant quantum computing, is on the order of microseconds at 100 K, comparable to the nitrogen-vacancy center in diamond10. For some systems, T2 is much shorter than T1, but if there is only an amplitude damping channel, then T2 is equal to 2T1. A long spin coherence time in vanadyl-Pc (1.04 microseconds) has also been observed even at room temperature, suggesting the potential of radical-bearing molecules for quantum gate operations11. In addition, organic molecules have major potential for QIP due to their scalability, portability, and tunability6,9. Recently, Bayliss et al. addressed the molecular spins for QIP in organic materials, using a small complex consisting of a chromium ion coordinated by aryl ligands6. The authors demonstrated the initialization, coherent control, and read-out of spin qubits by using optical excitations. In addition, the quantum teleportation of spin states at 85 K was demonstrated experimentally in a covalent donor-acceptor radical pair system12. More importantly, the incorporation of organic radicals (spin-\(\frac{1}{2}\), a natural candidate for qubits) into the QIP molecular architecture and further scalability improvements, facilitated by chemical synthesis and molecular engineering, are easier than their traditional inorganic counterparts13.

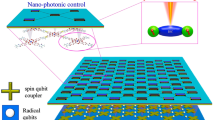
For radical-bearing molecules, the long-lived triplet (spin-1) can be formed by optical excitations and intersystem crossing (ISC, from the singlet excited state to the triplet ground state)14, which can interact via exchange interactions coherently with the radical spin. The triplet plays a role not only as a qutrit (a 3-level quantum system), which can lead to increased security, greater channel capacities, and more efficient gate operations7, but also a coupler for controlling the interaction between radicals15. Spin states such as a quartet (one radical coupled with a triplet), as shown in Fig. 1, or even higher spin states16 with multiple radicals can be produced, which have been observed by time-resolved electron paramagnetic resonance (TR-EPR) spectroscopy15,17,18,19,20,21,22. The electron spin coherence therein due to the exchange interaction at high temperature can be used for quantum gate operations. This exchange interaction, the strongest short-range interaction between electron spins, plays an essential role in spin-based QIP for producing coherence23,24,25. Teki et al. performed experimental and theoretical works on the exchange-coupled doublet-triplet molecular system26,27,28. The authors’ research focused on spin dynamics, spin polarization, and population transfers. The theoretical methods used therein for dealing with decoherence due to the environment are essentially semiclassical, whereas the system Hamiltonian is quantum26. Previously, the interaction between the doublet and triplet was studied theoretically based on perturbation theory up to the second order. These studies indicated the dependence of spin polarizations on the exchange interaction, magnetic field, and zero-field splitting. An interesting conclusion therein is that the net spin polarization for the doublet can still survive even after triplet relaxation29,30. In addition, CuPc molecules could serve as a good platform for optically controlled spin coherence at high temperature, as suggested by density functional theory calculations for the exchange interaction between the localized spin on the Cu ion and the triplet31. Theoretical validation of the optically controlled spin coherence in radical-bearing molecules can open a new avenue to achieve high-temperature QIP; thus, a general open quantum system model is mandatory for the realization of QIP at temperatures far above millikelvin.

Fig. 1: The optically induced entanglement between the triplet and the radical in a molecular system consisting of metal-free Pc (H2Pc) and a TEMPO radical is illustrated.
figure 1

This is only an example for illustration, and the actual system and experiment might be different and more challenging. Carbon is in gray, nitrogen is in blue, oxygen is in red, and hydrogen is in white. The triplet state is formed at the optically active (OA) moiety (H2Pc) after optical excitation with an appropriate frequency and ISC. Spin coherence is driven by the exchange interaction between the triplet and the radical.

Full size image

In this work, we proposed a general open quantum system model for triplet-radical pair systems (TRPSs), such as organic molecules containing one radical, as illustrated in Fig. 1. Here, we assumed that the molecules were sufficiently far apart such that we were equivalently dealing with an isolated single molecule consisting of a radical and a triplet, provided the molecular densities could still ensure a good signal in the TR-EPR experiment. We therefore neglected the explicit T2 effect in this work. Our numerical results based on the Markovian approximation within the weak coupling limit were qualitatively in good agreement with recent TR-EPR experiments on TRPSs32. Most importantly, our work suggested the feasibility of high-temperature quantum gate operations based on radical-bearing molecules.

System description and theoretical method

In TR-EPR experiments, the environment in which spin-bearing molecules are usually exposed is important for the description of spin dynamics, such as lattice vibrations (crucial for determining spin-lattice relaxation times). At temperatures even above the boiling point of liquid nitrogen, the spin-lattice relaxation time of a radical spin is typically ~microsecond, as in CuPc and N@C6010. ISC normally happens faster (transition time ~ nanosecond or transition rate ~10 mT) than spin-lattice relaxation owing to the spin-orbit interaction. ISC results in a very slow relaxation from the triplet state back to the singlet ground state, and the phosphorescence lifetime is ~millisecond. The static magnetic field is on the order of 100 mT, as found, for example, in typical X-band EPR spectroscopy (~9.5 GHz). Therefore, the Markovian description in the theory of open quantum systems (the weak coupling limit) could be a good approximation to describe the spin dynamics in TRPSs exposed to the environment33. Here, we established an effective spin Hamiltonian and a set of quantum jump operators, set up Liouville equations (and the corresponding superoperators—Liouvillians), and calculated the time evolution of the density matrices and the TR-EPR spectra.

Effective Hamiltonian

The effective spin Hamiltonian of a TRPS reads

$$\begin{array}{ll}\hat H_{{{{\mathrm{TRPS}}}}} = g_t\mu _B{{{\mathbf{B}}}} \cdot {{{\hat{\boldsymbol T}}}} + g_r\mu _B{{{\mathbf{B}}}} \cdot {{{\hat{\boldsymbol s}}}} + J{{{\hat{\boldsymbol s}}}} \cdot {{{\hat{\boldsymbol T}}}} + D\hat T_z^2\\ \qquad\qquad+\, E\left( {\hat T_x^2 - \hat T_y^2} \right)\end{array}$$
(1)

\({{{\hat{\boldsymbol T}}}}\) is the triplet spin-1 of the optically active (OA) moiety and \({{{\hat{\boldsymbol s}}}}\) the radical \(\frac{1}{2}\)-spin. The addition of the two spins leads to a total spin of \(\frac{1}{2}\) (a doublet, with a multiplicity of 2) and \(\frac{3}{2}\) (a quartet, with a multiplicity of 4). The first two terms are the Zeeman energies for the triplet and the radical with a static magnetic field of B, respectively. gt is the g-factor of the triplet spin, while gr is the radical spin. The third term is the exchange interaction (J) between the radical and the triplet. D and E are the zero-field splitting (ZFS) for the triplet, as shown in the last two terms. The triplet and radical spins are entangled when J is comparable with or larger than D and E.

If we combine the optical field with the effective Hamiltonian above (Eq. 1) and use the rotating wave approximation (RWA)34, we have

$$\begin{array}{ll}\hat H_{{\rm{TRPS}}}^{{\rm{OPT}}} = |T > [\hat H_{{\rm{TRPS}}}] < T| + |S_1 > \left[ {g_r\mu _B{{{\boldsymbol{B}}}} \cdot {{{\hat{\boldsymbol s}}}}} \right] < S_1|\\\qquad\quad + |S_0 > \left[ {g_r\mu _B{{{\boldsymbol{B}}}} \cdot {{{\hat{\boldsymbol s}}}}} \right] < S_0| + V\left( {|S_1 > < S_0| + |S_0 > < S_1|} \right)\end{array}$$
(2)

for a TRPS interacting with the optical field V. Here, S0 represents the singlet ground-state manifold, S1 is the excited singlet, and T is the triplet. The first term represents the interaction in a triplet manifold. The second and third terms are for the Zeeman energies of the radical when the OA moiety is in the singlet ground and excited states, respectively. The last term describes the optical excitation; here, V is the optical transition matrix element between the ground and excited singlet states (S0 and S1, respectively). Note that we used the bases \(|\frac{1}{2},\frac{1}{2}\rangle\,{{{\mathrm{and}}}}\) \(|\frac{1}{2}, - \frac{1}{2}\rangle\) for the radical spin and |1,1〉, |1,0〉, and |1,−1〉 for the triplet spin (the spin states are written in the form of |s,ms>〉). Compared with the traditional convention for the triplet (|+〉, |0〉, and |−〉), this choice of bases was beneficial for the QIP representation of the quantum states35. In addition, the molecular orientation has a crucial effect on the quantum state populations and EPR spectra36,37. In practice, the EPR spectra need to be simulated as the averaging effect due to the randomly distributed molecular orientations relative to the static magnetic field direction. However, in this work, we assumed that the molecular principal axis was along the z-direction of the static magnetic field; i.e., we neglected the orientation effect at the moment. In the future, we would like to perform theoretical work on the molecular orientation effect. Therein, we will compute and evaluate the molecular orientation effect on the quantum state populations and EPR spectra and the powder averaging for the random distribution of molecular orientations. We will also take into account the molecular aggregation effect determined by the molecular density and distributions (closely related to the spin-spin interactions between molecules), which is also important for the EPR spectra of spin-bearing molecules37.

Quantum jump operators

For the incoherent processes, we took into account the spin relaxations, the spontaneous decay of the singlet excited state, and the crossovers between the singlet excited and triplet states (ISC and the slow decay from the triplet state to singlet ground state). Figure 2 shows the transition processes in TR-EPR experiments for the TRPS. Therein, kST is the transition rate for ISC (from the singlet excited state to the triplet state), kEG is the rate for the spontaneous decay from the singlet excited to ground state and kTG is the rate for the decay from the triplet to singlet ground state.

Fig. 2: The energy level diagram for the TRPS and the transition processes between different states are shown.
figure 2

S refers to the spin state of the OA moiety in the molecule, while s is the radical spin. Stotal labels the total spin (S + s), which could be \(\frac{1}{2}\) or \(\frac{3}{2}\). kST is the ISC rate (the transition from S1 to T), kEG is the rate for the spontaneous decay from S1 to S0, and kTG is the decay rate from T to S0. Note that we assume here that the ISC and the transition from T to S0 are allowed only for the manifold with a total spin Stotal = \(\frac{1}{2}\).

Full size image

As shown in Fig. 2, the energy level diagram of different spin configurations, optical excitations and different relaxation and decay processes were included. We listed the Liouvillian operators that describe quantum jumps (incoherent processes) below. The superoperators constructed by the Lindblad operators were as follows:

$$\widehat {\hat L}_i\hat \rho = \mathop {\sum}\limits_{\mu = 1}^{n_i} {\gamma _\mu ^i\left[ {\hat l_\mu ^i\hat \rho \hat l_\mu ^{i{\dagger} } - \frac{1}{2}\left\{ {\hat \rho ,\hat l_\mu ^{i{\dagger} }\hat l_\mu ^i} \right\}} \right]}$$
(3)

Here, \(\hat \rho\) is the density matrix. The square bracket is the commutator, and the curly bracket is the anticommutator. For a TRPS, i = 1 to 5 (labeling different incoherent processes), the rate of the incoherent processes is described as \(\gamma _\mu ^i\), where μ labels different operators. \(\widehat {\hat L}_1\)with n1= 3 is used to describe the radical spin-\(\frac{1}{2}\) relaxation as follows: \(\hat l_1^1 = \hat s^ +\) (spin-\(\frac{1}{2}\) raising operator), \(\hat l_2^1 = \hat s^ -\)(spin-\(\frac{1}{2}\) lowering operator), and \(\hat l_3^1 = \hat s_z\) (the z-component of spin-\(\frac{1}{2}\)). The \(\hat s_z\) operator is responsible for the pure dephasing of quantum states, whereas \(\hat s^ +\) and \(\hat s^ -\) are responsible for random jumps. \(\widehat {\hat L}_2\) with n2 = 8 is used as a superoperator to describe the relaxation of the triplet state. We used the eight Gell-Mann matrices for these operators. Note that we implicitly included the transverse relaxation process corresponding to the T2 time in our Lindblad formalism through the pure dephasing Lindblad operators for both the radical and the triplet. Here, we accounted for the ISC; however, we assumed here that the total spin angular momentum was conserved, i.e., \({{{\boldsymbol{S}}}}_{{\rm{total}}} = \frac{1}{2}\), thus obtaining the following operators. \(\widehat{\hat L}_3\) with n3 = 2 is the superoperator describing the transition from the single excited state to the triplet state; \(\hat l_1^3 = |\frac{1}{2},\frac{1}{2} \,>\, _T \,<\, \frac{1}{2},\frac{1}{2}|_{S_1}\) and \(\hat l_2^3 = |\frac{1}{2}, - \frac{1}{2} \,>\, _T \,<\, \frac{1}{2}, - \frac{1}{2}|_{S_1}\). Similarly, we have \(\widehat {\hat L}_4\) with n4 = 2, which is the superoperator for the transition from the singlet excited to singlet ground state; \(\hat l_1^4 = |\frac{1}{2},\frac{1}{2} > _{S_0} < \frac{1}{2},\frac{1}{2}|_{S_1}\) and \(\hat l_2^4 = |\frac{1}{2}, - \frac{1}{2} > _{S_0} < \frac{1}{2}, - \frac{1}{2}|_{S_1}\), corresponding to spontaneous decay. \(\widehat{\hat L}_5\)where n5 = 2 is the superoperator that describes the transition from the triplet state to the singlet ground state; \(\hat l_1^5 = |\frac{1}{2},\frac{1}{2} > _{S_0} < \frac{1}{2},\frac{1}{2}|_T\) and \(\hat l_2^5 = |\frac{1}{2}, - \frac{1}{2} > _{S_0} < \frac{1}{2}, - \frac{1}{2}|_T\). \(\gamma _\mu ^i\) will be parametrized later.

The spin Hamiltonian operator and quantum jump operator (implemented through the Lindblad equation) can then be combined into the Liouville equation, or equivalently the Liouvillian formalism33. Therefore, the total Liouvillian superoperator is written as

$$\widehat {\hat {\frak{L}}}\hat \rho = - i\left[ {\hat H_{{\rm{TRPS}}}^{{\rm{OPT}}},\hat \rho } \right] + \left[ {\mathop {\sum}\nolimits_i {\widehat {\hat L}_i} } \right]\hat \rho$$
(4)

Here, the first part is the coherent interaction from the effective spin Hamiltonian and optical field (see Eq. 2). The second part includes the incoherent processes associated with the relaxations and crossovers between states (see Eq. 3). Therefore, we obtained a 10 by 10 Hamiltonian matrix (2 for the singlet ground state with the spin-\(\frac{1}{2}\) radical, 2 for the singlet excited states with the spin-\(\frac{1}{2}\) radical, 6 for the triplet state with radical), leading to a 100 by 100 Liouvillian matrix.

Linear response theory for TR-EPR spectra

For TR-EPR spectra, we adopted and generalized phenomenally the formalisms presented in refs. 38,39. Based on linear response theory, the intensities of the TR-EPR spectra were calculated as follows:

$$I\left( {t,\omega } \right) = \left|{\rm{Tr}}\left\{ {\hat \rho \left( t \right)\left[ {\hat T_x + \hat s_x} \right]\left[ {i\widehat {\hat {\frak{L}}} - \omega I} \right]^{ - 1}\left[ {\hat T_x + \hat s_x} \right]} \right\}\right|$$
(5)

Here, \(\hat \rho \left( t \right)\) is the time-dependent density matrix. \(\hat T_x + \hat s_x\)is the x-component of the total spin. ω is the frequency of the microwave field. I is the identity matrix. \(\widehat {\hat {\frak{L}}}\) is the superoperator (see Eq. 4).

Results and discussion

Here, we assumed that the radical and triplet had comparable spin-lattice relaxation rates, which were at ~MHz levels at the boiling point of liquid nitrogen10. ISC was fast (at a rate ~0.1 GHz). The system decayed very slowly from the triplet to the singlet ground state (at a rate ~kHz). We varied these parameters to carefully observe the effects of the spin relaxation rates on the TR-EPR spectra. Another important parameter was the exchange interaction between the radical and the triplet, which could not only be calculated by density functional theory but also estimated by fitting the experimental EPR spectra. We used millitesla (mT) as the unit of energy and relaxation rates throughout the paper. Here, we explored a set of values for the exchange interaction (either ferromagnetic or antiferromagnetic), including −10, −20, 20, and 50 mT. Our model could be used to predict the time evolution of density matrices and, more importantly, the two-dimensional TR-EPR spectra in the time and magnetic field domains.

The parameters used for calculations

Here, for ZFS, we assumed that D was 10 mT and E was 1 mT, which are the typical values for molecules16. To simplify our parameters, we assumed that gr = gt = 2.0. We also assumed that \({\upgamma}_i^1(i = 1 - 3) = k_{{{\mathrm{R}}}}\), \({\upgamma}_i^2(i = 1 - 8) = k_{{{\mathrm{T}}}}\),\({\upgamma}_1^3 = {\upgamma}_2^3 = k_{{{{\mathrm{ST}}}}}\), \({\upgamma}_1^4 = {\upgamma}_2^4 = k_{{{{\mathrm{EG}}}}}\), and \({\upgamma}_1^5 = {\upgamma}_2^5 = k_{{{{\mathrm{TG}}}}}\). Here, kR and kT are the relaxation rates for the radical and the triplet, respectively. The initial density matrix was chosen to be the thermalized classical mixture for the radical, i.e., \(\hat \rho _0 = \frac{1}{2}\left( {|\frac{1}{2},\frac{1}{2} > _{S_0} < \frac{1}{2},\frac{1}{2}|_{S_0} + |\frac{1}{2}, - \frac{1}{2} > _{S_0} < \frac{1}{2}, - \frac{1}{2}|_{S_0}} \right)\).

The spin entanglement generation process can be elucidated by comparing our calculations with experiments. In the coherent part, we had D = 10 mT, E =1 mT, J = −10 mT, and V = 10 mT. We also estimated the incoherent parameters for the high temperature as follows: kR = 0.1 mT, kT = 0.1 mT, kST = 10 mT, kTG = 0.0001 mT, and kEG = 0.01 mT. The magnetic field ranged between 280 mT and 420 mT.

Time evolution of the density matrix

First, we simulated the time evolution of the density matrix up to ~200 ps from time 0, when an optical excitation was applied. As shown in Fig. 3, we computed the time evolution of the populations (the diagonal terms of the density matrix, for the excited states \(|0,0\rangle_e|\frac{1}{2},\frac{1}{2}\rangle\), \(|1,0\rangle|\frac{1}{2},\frac{1}{2}\rangle\), and \(|1, - 1\rangle|\frac{1}{2},\frac{1}{2}\rangle\), and the ground state \(|0,0\rangle_g|\frac{1}{2},\frac{1}{2}\rangle\), which corresponded to \(\rho _{11},\rho _{44},\rho _{66},\) and ρ99, respectively). Here, the first bracket was for the singlet/triplet manifold (the singlet excited state labeled by e, the ground state by g) of the OA moiety of the molecule, and the second bracket was for the radical spin. The absolute values of the corresponding off-diagonal terms (|ρ19| and |ρ46|), which characterized the coherence, were calculated.

Fig. 3: The time evolutions of the matrix elements are shown.
figure 3

a The populations of spin state \(|0,0\rangle_e|\frac{1}{2},\frac{1}{2}\rangle\) are shown in blue, while spin state \(|0,0\rangle_g|\frac{1}{2},\frac{1}{2}\rangle\) is shown in black. The off-diagonal term between the above two states is shown in red. b The populations of the spin states \(|1,0\rangle|\frac{1}{2},\frac{1}{2}\rangle\) and \(|1,1\rangle|\frac{1}{2}, - \frac{1}{2}\rangle\) are shown in blue and black, respectively, and the off-diagonal term between the two states is shown in red. All the matrix elements of these states shown here exhibit Rabi oscillation, implying coherence induced by the optical excitations. All the parameters used are listed in the main text. (c) The time evolutions of the populations of the spin state \(|1,0\rangle|\frac{1}{2},\frac{1}{2}\rangle\) are shown. The red curve is for the exchange interaction J = −10 mT and the blue curve for J = −20 mT. We can see that within this energy range, the oscillation frequency for the population increases with the exchange interaction. This behavior suggests a correlation between coherent oscillations and the exchange interaction.

Full size image

We can see the Rabi oscillations of the populations and the off-diagonal terms for the states in Fig. 3, which suggested that spin coherence could be produced by using this optically driven process, starting from a classical mixture state of the radical spin. The resulting entanglement between the radical and the triplet provides the foundation for the QIP application of the proposed molecular architecture. The populations of \(|0,0\rangle_e|\frac{1}{2},\frac{1}{2}\rangle\) and \(|0,0\rangle_g|\frac{1}{2},\frac{1}{2}\rangle\) (the blue and black curves in Fig. 3a, respectively) oscillated in the beginning but decayed very fast. These oscillatory processes for the states \(|0,0\rangle_g|\frac{1}{2},\frac{1}{2}\rangle\) and \(|0,0\rangle_e|\frac{1}{2},\frac{1}{2}\rangle\) were mainly driven by the external optical excitations. The oscillating populations for the states \(|1,0\rangle|\frac{1}{2},\frac{1}{2}\rangle\) and \(|1,1\rangle|\frac{1}{2}, - \frac{1}{2}\rangle\) and the off-diagonal term (the blue, black, and red curves in Fig. 3b, respectively) suggested that spin coherence was driven by the exchange interaction and the external optical excitations, leading to the entangled state between spin-\(\frac{1}{2}\) and the triplet. From these analyses, with the chosen parameters, we also observed that the populations were cumulated to the sextet states (the right-hand-side part in Fig. 2) formed by the radical and the triplet because of a fast ISC rate and a strong optical driving field but a slow decay back down to the singlet ground state. However, the coherence eventually vanishes after removing the optical driving, owing to the decay of the triplet to the singlet ground state.

As shown in Fig. 3c, we compared the time evolutions of the population of the spin state \(|1,0\rangle|\frac{1}{2},\frac{1}{2}\rangle\) for the exchange interaction equal to −10 mT (the red curve) and −20 mT (the blue curve). The oscillation frequency increased with increasing magnitude of the exchange interaction. This comparison suggested that the oscillatory behavior of the populations (and coherence) for the states \(|1,0\rangle|\frac{1}{2},\frac{1}{2}\rangle\) and \(|1,1\rangle|\frac{1}{2}, - \frac{1}{2}\rangle\)) was driven mainly by the exchange interaction, assisted by the optical driving field.

Figure 4 presents the tomography of the sextet density matrix at the early stage (T = 6.2 ps), which clearly shows the nonzero off-diagonal terms (coherence) after optical excitation. Here, \(|1\rangle = |1,1\rangle|\frac{1}{2}\rangle,\frac{1}{2}\rangle\), \(|2\rangle = |1,0\rangle|\frac{1}{2},\frac{1}{2}\rangle\), \(|3\rangle = |1, - 1\rangle|\frac{1}{2},\frac{1}{2}\rangle\), \(|4\rangle = |1,1\rangle|\frac{1}{2}, - \frac{1}{2}\rangle\), \(|5\rangle = |1,0\rangle|\frac{1}{2}, - \frac{1}{2}\rangle\), and \(|6\rangle = |1, - 1\rangle|\frac{1}{2}, - \frac{1}{2}\rangle\).

Fig. 4: The tomography of the density matrix for the sextet at the early stage (T = 6.2 ps) is shown.
figure 4

Nonzero off-diagonal terms (coherence) are clearly shown in gray.

Full size image

TR-EPR spectra

The response function of the open quantum system was the essential part of our TR-EPR simulations, as shown in Eq. 5.

As shown in Fig. 5, we computed the TR-EPR spectra at the early stage of the evolution (T = 6.2 ps). As the exchange interaction increased, i.e., J = −10 mT, 20 mT, and 50 mT for Fig. 5 (a-c), respectively, we observed a widening range of the EPR spectra. Some of the side peaks stemmed from the triplet spin anisotropy characterized by D and E. On the other hand, the outer peaks far from the middle were attributed to the exchange interaction. The central peaks were from the quartet components (the total spin = \(\frac{3}{2}\)) when the spin-\(\frac{1}{2}\) and triplet were coupled. Previous studies assigned the lower-energy peaks to the ground state and the middle- and higher-energy peaks to the excited states16, which implies that the gaps between these peaks will become larger as we increase the exchange interaction. Hence, the widening of the spectral range with the exchange interaction as determined by our calculations was consistent with this picture16. In Fig. 5(d), we used the same parameters as in Fig. 3 but increased the magnitudes for kR and kT to 1 mT. We can see that the line widths of the EPR spectra were broadened as these processes were incoherent. In addition, compared with the previous work for the experiments on ZnTPP-3-Nopy and MgTPP-Nitpy by Ishii et al.40 and porphyrin-trityl systems evaluated by Nolden et al.33, we had very good qualitative agreement with the experimental TR-EPR spectra therein.

Fig. 5: The TR-EPR spectra at the early stage (T = 6.2 ps) as a function of magnetic field are shown with different exchange interactions and relaxation rates.
figure 5

a J = −10 mT, (b) J = 20 mT, and (c) J = 50 mT, where the red arrows indicate the energy range for the nonzero spectra. In the inset of (c), we also show the zoom-in of the spectra for the magnetic field between 380 mT and 400 mT. In (d), the TR-EPR spectra for kT =1.0 mT and kR=1.0 mT are shown in red and blue, respectively, compared with those in (a) (black). As the exchange interaction increases, the range of the EPR spectra broadens, suggesting the widening effect of the exchange interactions on the spectra. The peak in the middle corresponds to the response to the quartet manifold in the sextet state. The side peaks are related to the ZFS of the triplet. We can also clearly see the broadening effect due to the increased relaxation rates in (d).

Full size image

Figure 6 shows a two-dimensional density plot of the calculated TR-EPR spectra (by using the parameters in Fig. 3) as a function of the magnetic field and time. Here, we turned on the optical field from time = 0 to 6.2 ps and then switched it off to observe the time evolution. As shown in Fig. 6, the TR-EPR spectra signals became stronger as the time evolved within this time range (from 0 to 6.2 ps) but decayed without optical driving. The T2 process has been implicitly included in our Lindblad formalism, such as the pure dephasing Lindblad operators. However, based on the work here, it is also worth accounting explicitly for the T2 process in our model and combining the modeling methodology in EasySpin with the theory of open quantum systems used here36. This work will be carried out in the future and presented in a separate publication. In this forthcoming work, we will also extend the simulation time scale to at least nanoseconds to observe the evolution of entanglement, which is very sensitive to the T2 time.

Fig. 6: The density plot of the TR-EPR spectra is shown as a function of magnetic field and time.
figure 6

Note that the signal starts to decay after we turn off the optical field.

Full size image

Conclusions

In summary, we proposed a general model for the spin dynamics and entanglement of a triplet-radical-pair molecular system based on the Markovian approximation in the theory of open quantum systems. The spin entanglement, implied by the Rabi oscillation characteristics of the density matrix elements owing to the exchange interaction between the triplet and the radical, could be manipulated and controlled by using optical excitations. The computed TR-EPR spectra based on the realistic experimental parameters for organic molecules were qualitatively in good agreement with those from previous experiments on radical-bearing molecules, which theoretically demonstrated a potential route to realize quantum gate operation between qubits and optically accessible qutrits by using organic molecular materials. Our work, in good agreement with recent TR-EPR experimental investigations, showed that optically addressable spin entanglement in radical-bearing molecular materials and architectures is promising for the realization of high-temperature QIP.