Introduction

The entropy production rate is an important quantitative measure of a non-equilibrium process and knowing its value is indicative of useful information about the system such as heat dissipated1,2, efficiency (if the non-equilibrium system in question is an engine3,4,5) as well as free energy differences6,7 (if the non-equilibrium process interpolates between two equilibrium states). In particular, the entropy production rate often characterizes the energy consumption of non-equilibrium systems8. It also provides useful information for systems with hidden degrees of freedom9,10, or interacting subsystems where information-theoretic quantities play a key role11,12,13,14.

The entropy production rate can be directly obtained from the system’s phase-space trajectory if the underlying dynamical equations of the system are known15,16,17,18. This is not the case however for the vast majority of systems, such as biological systems19,20,21, and consequently, there has been a lot of interest in developing new methods for estimating the entropy production rate directly from trajectory data22,23,24,25,26,27,28,29,30,31,32,33. Some of these techniques involve the estimation of the probability distribution and currents over the phase-space22,26, which requires huge amounts of data. Some other techniques are invasive and require perturbing the system1,2, which may not always be easy to implement.

An alternative strategy is to set lower bounds on the entropy production rate34,35,36,37,38 by measuring experimentally accessible quantities. One class of these bounds, for example, those based on the thermodynamic uncertainty relation (TUR)38,39,40,41,42, have been further developed into variational inference schemes which translate the task of identifying entropy production to an optimization problem over the space of a single projected fluctuating current in the system26,27,28,29. Recently a similar variational scheme using neural networks was also proposed30. As compared to other trajectory-based entropy estimation methods, these inference schemes do not involve the estimation of any kind of empirical distributions over the phase-space and are hence known to work better in higher dimensional systems26. In addition, it is proven that such an optimization problem gives the exact value of the entropy production rate in a stationary state if short-time currents are used27,28,29,30. The short-time TUR has also been experimentally tested in colloidal particle systems recently43. However, whether these existing schemes work well for non-stationary states has not been explored as yet.

Non-stationary dynamics ubiquitously appear in biological phenomena such as in adaptive responses to environmental change44 and spontaneous oscillations45, all of which are inevitably accompanied by energy dissipation. However, for a non-stationary system, it has only been possible to place bounds on the time-dependent entropy produced during a finite time interval under specific46,47 or more general48 conditions. In addition, there is no guarantee that these bounds can be saturated by any quantity related to the entropy production of the system. Hence there is no established scheme that has been proven to work for obtaining the exact entropy production rate under time-dependent conditions.

Here, we address this problem by proposing a class of variational inference schemes that can give the exact value of the time-dependent entropy production rate under non-stationary conditions as well as the entropy production along with single realizations. These schemes, which can be directly implemented on time-series data obtained from experiments, involve maximization over an objective function that consists of a single projected current determined from the data. We demonstrate that this objective function can either be of the form dictated by the recently proposed short-time TUR27,28,29 or the form recently suggested in30, or a variation of these. The collection of these schemes works for both diffusive systems described by overdamped Langevin equations as well as finite-state-space systems described by master equations and work for both transients as well as stationary states.

We implement these variational schemes by means of an efficient algorithm that estimates the entropy production continuously in time by modeling the time-dependent projection coefficients with a feedforward neural network and by carrying out gradient ascent using machine learning techniques. This algorithm can in principle be directly used on real experimental data. As a proof of concept, here we consider time-series data generated by two models; one of a colloidal particle in a time-varying trap and the other of a biological model that describes biochemical reactions affected by a time-dependent input signal, for both of which we can obtain exact solutions for the time-dependent entropy production rate as well as the entropy production along single trajectories. We then demonstrate that our proposed scheme indeed works by comparing the numerical implementation to our theoretical predictions (see Fig. 1).

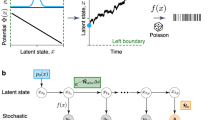
Fig. 1: Estimating the entropy production along non-stationary trajectories.
figure 1

a Schematic of our inference scheme. The box on the left displays a trajectory generated by the breathing parabola model in which a fluctuating colloidal particle (orange circle) inside a harmonic trap is driven out of equilibrium as the stiffness of the trap decreases. The system parameters for the simulations shown here are: the parameter for the protocol of the changing stiffness α = 11.53, the diffusion constant D = 1.6713 × 10−13, the time interval of trajectories Δt = 10−2, and the observation time τobs = 1. The position at time t is described as xt. The box on the right displays the steps in our inference scheme: we train the model function d(x, t∣θ) with parameters θ to get the optimal values θ*, and use them for estimating the (single-step) entropy production \({{\Delta }}\widehat{S}\). b Estimated entropy production along a single trajectory. The dashed green line is the estimated entropy production, and the solid black line is the true entropy production calculated analytically. The estimation is conducted for the trajectory depicted in panel (a) after training the model function using 105 trajectories. The blue circles (variance-based estimator (Eq. (14)) and green triangles (simple dual representation (Eq. (10)) are the estimated entropy production rate using (c) 104 or (d) 105 trajectories, and the black line is the true value. The model function is trained with the simple dual representation in both cases. As is evident, the variance-based estimator reduces the statistical error significantly. In (c) and (d), the mean of ten independent trials are plotted for the estimated values, and the error bars correspond to the standard deviation divided by \(\sqrt{10}\).

Full size image

Results

Short-time variational representations of the entropy production rate

The central results we obtain, summarized in Fig. 1, are applicable to experimental data from any non-equilibrium system, at least in principle, described by an overdamped Langevin equation or a Markov jump process even without knowing any details of the equations involved. Here, we use the model of a generic overdamped Langevin dynamics in d-dimensions in order to introduce the notations. We consider an equation of the form:

$$\dot{{{{{{{{\boldsymbol{x}}}}}}}}}(t)={{{{{{{\boldsymbol{A}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}}(t),t)+{{{{{{{\boldsymbol{B}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}}(t),t)\cdot {{{{{{{\boldsymbol{\eta }}}}}}}}(t),$$
(1)

where A(x, t) is the drift vector, and B(x, t) is a d × d matrix, and η(t) represents a Gaussian white noise satisfying \(\langle {\eta }_{i}(t){\eta }_{j}(t^{\prime} )\rangle ={\delta }_{ij}\delta (t-t^{\prime} )\). Note that we adopt the Ito-convention for the multiplicative noise. The corresponding Fokker-Planck equation satisfied by the probability density p(x, t) reads

$${\partial }_{t}p({{{{{{{\boldsymbol{x}}}}}}}},t)=-{{{{{{{\boldsymbol{\nabla }}}}}}}}\ {{{{{{{\boldsymbol{j}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}},t),$$
(2)
$${j}_{i}({{{{{{{\boldsymbol{x}}}}}}}},t)={A}_{i}({{{{{{{\boldsymbol{x}}}}}}}},t)p({{{{{{{\boldsymbol{x}}}}}}}},t)-\mathop{\sum}\limits_{j}{\nabla }_{j}\left[{D}_{ij}({{{{{{{\boldsymbol{x}}}}}}}},t)p({{{{{{{\boldsymbol{x}}}}}}}},t)\right],$$
(3)

where D is the diffusion matrix defined by

$$\begin{array}{r}{{{{{{{\boldsymbol{D}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}},t)=\frac{1}{2}{{{{{{{\boldsymbol{B}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}},t){{{{{{{\boldsymbol{B}}}}}}}}{({{{{{{{\boldsymbol{x}}}}}}}},t)}^{T}\end{array}$$
(4)

and j(x, t) is the probability current. Equations of the form Eq. (2) can, for example, be used to describe the motion of colloidal particles in optical traps49,50,51,52. In some of these cases, the Fokker-Planck equation can also be solved exactly to obtain the instantaneous probability density p(x, t).

Whenever j(x, t) ≠ 0, the system is out of equilibrium. How far the system is from equilibrium can be quantified using the average rate of the entropy production at a given instant σ(t), which can be formally obtained as the integral53

$$\sigma (t)=\int {{{{{{{\rm{d}}}}}}}}{{{{{{{\boldsymbol{x}}}}}}}}\ {{{{{{{\boldsymbol{F}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}},t)\ {{{{{{{\boldsymbol{j}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}},t),$$
(5)

where F(x, t) is the thermodynamic force defined as

$${{{{{{{\boldsymbol{F}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}},t)=\frac{{{{{{{{{\boldsymbol{j}}}}}}}}}^{T}({{{{{{{\boldsymbol{x}}}}}}}},t){{{{{{{\boldsymbol{D}}}}}}}}{({{{{{{{\boldsymbol{x}}}}}}}},t)}^{-1}}{p({{{{{{{\boldsymbol{x}}}}}}}},t)}.$$
(6)

Note that the Boltzmann’s constant is set to unity kB = 1 throughout this paper. Further, the entropy production along a stochastic trajectory denoted as S[x( ⋅ ), t] can be obtained as the integral of the single-step entropy production

$$\begin{array}{r}{{{{{{{\rm{d}}}}}}}}S={{{{{{{\boldsymbol{F}}}}}}}}\left({{{{{{{\boldsymbol{x}}}}}}}}(t),t\right)\circ {{{{{{{\rm{d}}}}}}}}{{{{{{{\boldsymbol{x}}}}}}}}(t),\end{array}$$
(7)

where ∘ denotes the Stratonovich product. This quantity is related to the average entropy production rate as σ(t) = 〈dS(t)/dt〉, where 〈 ⋯ 〉 denotes the ensemble average. Similar expressions can be obtained for any Markov jump processes if the underlying dynamical equations are specified17.

In the following, we discuss two variational representations that can estimate σ(t), F(x, t), and S[x( ⋅ ), t] in non-stationary systems, without requiring prior knowledge of the dynamical equation. We also construct a third simpler variant and comment on the pros and cons of these different representations for inference.

TUR representation

The first method is based on the TUR26,38,39,40,41,42, which provides a lower bound for the entropy production rate in terms of the first two cumulants of non-equilibrium current fluctuations directly measured from the trajectory. It was shown recently that the TUR provides not only a bound, but even an exact estimate of the entropy production rate for stationary overdamped Langevin dynamics by taking the short-time limit of the current27,28,29. Crucially, the proof in Ref. 28 is also valid for non-stationary dynamics.

This gives a variational representation of the entropy production rate, given by the estimator

$${\sigma }_{{{{{{{{\rm{TUR}}}}}}}}}(t):= \frac{1}{{{{{{{{\rm{d}}}}}}}}t}\mathop{\max }\limits_{{{{{{{{\boldsymbol{d}}}}}}}}}\frac{2{ \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle }^{2}}{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})},$$
(8)

where Jd is the (single-step) generalized current given by Jd ≔ d(x(t)) ∘ dx(t) defined with some coefficient field d(x). The expectation and the variance are taken with respect to the joint probability density p(x(t), x(t + dt)). In the ideal short-time limit dt → 0, the estimator gives the exact value, i.e., σTUR(t) = σ(t) holds28. The optimal current that maximizes the objective function is proportional to the entropy production along a trajectory, \({J}_{{{{{{{{\boldsymbol{d}}}}}}}}}^{* }=c{{{{{{{\rm{d}}}}}}}}S\), and the corresponding coefficient field is d*(x) = cF(x, t), where the constant factor c can be removed by calculating \(2 \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle /{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})=1/c\).

NEEP representation

The second variational scheme is the Neural Estimator for Entropy Production (NEEP) proposed in Ref. 30. In this study, we define the estimator σNEEP in the form of a variational representation of the entropy production rate as

$${\sigma }_{{{{{{{{\rm{NEEP}}}}}}}}}(t):= \frac{1}{{{{{{{{\rm{d}}}}}}}}t}\mathop{\max }\limits_{{{{{{{{\boldsymbol{d}}}}}}}}} \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}}-{e}^{-{J}_{{{{{{{{\boldsymbol{d}}}}}}}}}}+1 \rangle ,$$
(9)

where the optimal current is the entropy production itself, \({J}_{{{{{{{{\boldsymbol{d}}}}}}}}}^{* }={{{{{{{\rm{d}}}}}}}}S\), and the corresponding coefficient field is d*(x) = F(x, t). Again, in the ideal short-time limit, σNEEP(t) = σ(t) holds. Eq. (9) is a slight modification of the variational formula obtained in Ref. 30; we have added the third term so that the maximized expression itself gives the entropy production rate. Although it was derived for stationary states there, it can be shown that such an assumption is not necessary in the short-time limit. We provide proof of our formula using a dual representation of the Kullback–Leibler divergence54,55,56 in Supplementary Note 2.

In contrast to the TUR representation, NEEP requires the convergence of exponential averages of current fluctuations, but it provides an exact estimate of the entropy production rate not only for diffusive Langevin dynamics but also for any Markov jump process. Since there are some differences in the estimation procedure for these cases28,30, we focus on Langevin dynamics in the following, while its use in Markov jump processes is discussed in Supplementary Note 2.

Simple dual representation

For Langevin dynamics, we also derive a new representation, named the simple dual representation σSimple by simplifying \(\langle {e}^{-{J}_{{{{{{{{\boldsymbol{d}}}}}}}}}} \rangle\) in the NEEP estimator as

$${\sigma }_{{{{{{{{\rm{Simple}}}}}}}}}(t):= \frac{1}{{{{{{{{\rm{d}}}}}}}}t}\mathop{\max }\limits_{{{{{{{{\boldsymbol{d}}}}}}}}}\left[2 \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle -\frac{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})}{2}\right].$$
(10)

Here, the expansion of \(\langle {e}^{-{J}_{{{{{{{{\boldsymbol{d}}}}}}}}}} \rangle\) in terms of the first two moments is exact only for Langevin dynamics and hence this representation cannot be used for Markov jump processes to obtain σ (however, as shown in57, the equivalence of the TUR objective function to the objective function in the above representation continues to hold in the long-time limit). The tightness of the simple dual and TUR bounds can be compared as follows: In Langevin dynamics, for any fixed choice of Jd,

$$\sigma {{{{{{{\rm{d}}}}}}}}t\ge \frac{2{ \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle }^{2}}{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})}\ge 2 \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle -\frac{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})}{2},$$
(11)

where we used the inequality \(\frac{2{a}^{2}}{b}\ge 2a-\frac{b}{2}\) for any a and b > 0. Since a tighter bound is advantageous for the estimation56,58, σTUR would be more effective for estimating the entropy production rate for the Langevin case.

On the other hand, σNEEP and σSimple have an advantage over σTUR in estimating the thermodynamic force F(x, t), since the optimal coefficient field is the thermodynamic force itself for these estimators. In contrast, σTUR needs to cancel the constant factor c by calculating \(2 \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle /{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})=1/c\), which can increase the statistical error due to the fluctuations of the single-step current (see Supplementary Note 2 for further discussions and numerical results). In the next section, we propose a continuous-time inference scheme that estimates in one shot, the time-dependent thermodynamic force for the entire time range of interest. This results in an accurate estimate with less error than the fluctuations of the single-step current. σNEEP and σSimple are more effective for this purpose, since the correction of the constant factor c, whose expression is based on the single-step current, negates the benefit of the continuous-time inference for σTUR. In Table 1, we provide a summary of the three variational representations.

Table 1 A summary of the comparison between the different variational representations considered in this work. σNEEP is the Neural Estimator for Entropy Production (NEEP) representation (Eq. (9)), σSimple is the simple dual representation (Eq. (10)), and σTUR is the thermodynamic uncertainty relation (TUR) based representation (Eq. (8)). They have different applicabilities to Markov jump processes and Langevin dynamics. The optimal coefficient field d*(x) that maximizes a variational representation is equivalent to or proportional to the thermodynamic force F(x, t). The TUR representation is the tightest as shown in Eq. (11).
Full size table

We note that the variational representations are exact only when all the degrees of freedom are observed; otherwise, they give a lower bound on the entropy production rate. This can be understood as an additional constraint on the optimization space. For example, when the i-th variable is not observed, it is equivalent to dropping xi from the argument of d(x) and setting di = 0. We also note that the variational representations are exact to order dt; in practice, we use a short but finite dt. The only variational representation which can give the exact value with any finite dt is σNEEP, under the condition that the dynamics are stationary30.

An algorithm for non-stationary inference

The central idea of our inference scheme is depicted in Fig. 1a. Equations (8), (9), and (10) all give the exact value of σ(t) in principle in the Langevin case, but here, we elaborate on how we implement them in practice. We first prepare an ensemble of finite-length trajectories, which are sampled from a non-equilibrium and non-stationary dynamics with Δt as the sampling interval:

$${{{\Gamma }}}_{i}=\left\{{{{{{{{{\boldsymbol{x}}}}}}}}}_{0}^{(i)},{{{{{{{{\boldsymbol{x}}}}}}}}}_{{{\Delta }}t}^{(i)},...,{{{{{{{{\boldsymbol{x}}}}}}}}}_{{\tau }_{{{{{{{{\rm{obs}}}}}}}}}}^{(i)}(={{{{{{{{\boldsymbol{x}}}}}}}}}_{M{{\Delta }}t}^{(i)})\right\}\,(i=1,...,N).$$
(12)

Here, i represents the index of trajectories, N is the number of trajectories, and M is the number of transitions. The subscript (i) will be often omitted for simplicity. Then, we estimate the entropy production rate σ(t) using the ensemble of single transitions \({\{{{{{{{{{\boldsymbol{x}}}}}}}}}_{t},{{{{{{{{\boldsymbol{x}}}}}}}}}_{t+{{\Delta }}t}\}}_{i}\) at time t. σ(t) is obtained by finding the optimal current that maximizes the objective function which is itself estimated using the data. Hereafter, we use the hat symbol for quantities estimated from the data: for example, \({\widehat{\sigma }}_{{{{{{{{\rm{Simple}}}}}}}}}(t)\) is the estimated objective function of the simple dual representation. We also use the notation \(\widehat{\sigma }(t)\) when the explanation is not dependent on the particular choice of the representation. The time interval for estimating \(\widehat{\sigma }(t)\) is set to be equal to the sampling interval Δt for simplicity, but they can be different in practice, i.e., transitions {xt, xt+nΔt} with some integer n≥1 can be used to estimate \(\widehat{\sigma }(t)\) for example.

Concretely, we can model the coefficient field with a parametric function d(x∣θ) and conduct the gradient ascent for the parameters θ. As will be explained, we use a feedforward neural network for the model function, where θ represents, for example, weights and biases associated with nodes in the neural network. In this study, we further optimize the coefficient field continuously in time, i.e., optimize a model function d(x, t∣θ) which includes time t as an argument. The objective function to maximize is then given by

$$f({{{{{{{\boldsymbol{\theta }}}}}}}}):= \frac{1}{M}\mathop{\sum }\limits_{j=0}^{M-1}\widehat{\sigma }(j{{\Delta }}t).$$
(13)

The optimal model function d(x, t∣θ*) that maximizes the objective function is expected to approximate well the thermodynamic force F(x, t) (or c(t)F(x, t) if σTUR is used) at least at jΔt(j = 0, 1, . . . ), and even at interpolating times if Δt is sufficiently small. Here, θ* denotes the set of optimal parameters obtained by the gradient ascent, and we often use d* to denote the optimal model function d(x, t∣θ*) hereafter.

This continuous-time inference scheme is a generalization of the instantaneous-time inference scheme. Instead of optimizing a time-independent model function d(x∣θ) in terms of \(\widehat{\sigma }(j{{\Delta }}t)\) with a fixed index j, the continuous-time scheme needs to perform only one optimization of the sum Eq. (13). This makes it much more data efficient in utilizing the synergy between ensembles of single transitions at different times. This also ensures that we can get the smooth change of the thermodynamic force, interpolating discrete-time transition data.

Variance-based estimator

In principle, all the three variational representations work as an estimator of the entropy production rate as well. However, as we detail in Supplementary Note 2, once we have obtained an estimate of the thermodynamic force d* ≃ F (taking into account the correction term for \({\widehat{\sigma }}_{{{{{{{{\rm{TUR}}}}}}}}}\)) by training the model function, it is possible to use a variance-based estimator of the entropy production rate,

$$\frac{1}{2{{{{{{{\rm{d}}}}}}}}t}{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{{d}}}}}}}^{* }}}})\simeq \frac{1}{2{{{{{{{\rm{d}}}}}}}}t}{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{F}}}}}}}}})=\sigma (t),$$
(14)

which can considerably reduce the statistical error. This is due to the fact that \(\widehat{ \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle }\) fluctuates around \(\langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle\) more than \(\widehat{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})}\) does around Var(Jd) for any choice of d, for small dt (see Supplementary Note 2 for the derivation). The above advantage in using the variance as an estimator, instead of the mean, would normally be masked by noise in the estimation of d*. However, if the coefficient field is trained by \({\widehat{\sigma }}_{{{{{{{{\rm{Simple}}}}}}}}}\) or \({\widehat{\sigma }}_{{{{{{{{\rm{NEEP}}}}}}}}}\) with the continuous-time inference scheme, remarkably, d* is obtained with an accuracy beyond the statistical error of \(\widehat{ \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle }\) since it takes the extra constraint of time continuity into account. This results in the error of \(\widehat{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{{d}}}}}}}^{* }}}})}\) being smaller than that of \(\widehat{ \langle {J}_{{{{{{{{\boldsymbol{{d}}}}}}}^{* }}}} \rangle }\), because of the difference in how the leading-order terms of their statistical fluctuation scale with dt. We note that \({\widehat{\sigma }}_{{{{{{{{\rm{TUR}}}}}}}}}\) is not appropriate for this purpose, since in this case, d* should be multiplied by \(2\widehat{ \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle }/\widehat{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})}\) to obtain an estimate of the thermodynamic force, which increases the statistical error to the same level as \(\widehat{ \langle {J}_{{{{{{{{\boldsymbol{d}}}}}}}}} \rangle }\).

In numerical experiments, we mainly use \({\widehat{\sigma }}_{{{{{{{{\rm{Simple}}}}}}}}}\) for training the coefficient field to demonstrate the validity of this new representation and use the variance-based estimator for estimating the entropy production rate.

We adopt the data splitting scheme28,30 for training the model function to avoid the underfitting and overfitting of the model function to trajectory data. Concretely, we use only half the number of trajectories for training the model function, while we use the other half for evaluating the model function and estimating the entropy production. In this scheme, the value of the objective function calculated with the latter half (we call it test value) quantifies the generalization capability of the trained model function. Thus, we can compare two model functions, and expect that the model function with the higher test value gives a better estimate. We denote the optimal parameters that maximize the test value during the gradient ascent as θ*. Hyperparameter values are obtained similarly. Further details, including a pseudo code, are provided in Supplementary Note 1.

Numerical results

We demonstrate the effectiveness of our inference scheme with the following two linear Langevin models: (i) a one-dimensional breathing parabola model, and (ii) a two-dimensional adaptation model. In both models, non-stationary dynamics are repeatedly simulated with the same protocol, and a number of trajectories are sampled. We estimate the entropy production rate solely on the basis of the trajectories and compare the results with the analytical solutions (see Supplementary Note 3 for the analytical calculations). Here, these linear models are adopted only to facilitate comparison with analytical solutions, and there is no hindrance to applying our method to nonlinear systems as well28.

We first consider the breathing parabola model that describes a one-dimensional colloidal system in a harmonic-trap \(V(x,t)=\frac{\kappa (t)}{2}{x}^{2}\), where κ(t) is the time-dependent stiffness of the trap. This is a well-studied model in stochastic thermodynamics49,50,59 and has been used to experimentally realize microscopic heat engines consisting of a single colloidal particle as the working substance60,61. The dynamics can be accurately described by the following overdamped Langevin equation:

$$\dot{x}(t)=-\frac{\kappa (t)}{\gamma }x(t)+\sqrt{2D}\ \eta (t).$$
(15)

Here γ is the viscous drag, and η is Gaussian white noise. We consider the case that the system is initially in equilibrium and driven out of equilibrium as the potential changes with time. Explicitly, we consider a protocol, κ(t) = γα/(1 + αt), where the parameters α, γ as well as the diffusion constant D are chosen such that they correspond to the experimental parameter set used in60 (see Supplementary Note 3).

In Fig. 1, we illustrate the central results of this paper for the breathing parabola model. We consider multiple realizations of the process of time duration τobs as time-series data (Fig. 1a). The inference takes this as input and produces as output the entropy production at the level of an individual trajectory \(\widehat{S}(t)\) for any single choice of realization (Fig. 1b), as well as the average entropy production rate \(\widehat{\sigma }(t)\) (Fig. 1c, d). Here, the entropy production along a single trajectory \(\widehat{S}(t)\) is estimated by summing up the estimated single-step entropy production:

$${{\Delta }}\widehat{S}(t):= {{{{{{{\boldsymbol{d}}}}}}}}\left(\frac{{{{{{{{{\boldsymbol{x}}}}}}}}}_{t}+{{{{{{{{\boldsymbol{x}}}}}}}}}_{t+{{\Delta }}t}}{2},t+\frac{{{\Delta }}t}{2}\,\bigg|{{{{{{{{\boldsymbol{\theta }}}}}}}}}^{* }\right)\ ({{{{{{{{\boldsymbol{x}}}}}}}}}_{t+{{\Delta }}t}-{{{{{{{{\boldsymbol{x}}}}}}}}}_{t}),\,\,$$
(16)

while the true entropy production S(t) is calculated by summing up the true single-step entropy production:

$${{\Delta }}S(t):= {{{{{{{\boldsymbol{F}}}}}}}}\left(\frac{{{{{{{{{\boldsymbol{x}}}}}}}}}_{t}+{{{{{{{{\boldsymbol{x}}}}}}}}}_{t+{{\Delta }}t}}{2},t+\frac{{{\Delta }}t}{2}\right)\ ({{{{{{{{\boldsymbol{x}}}}}}}}}_{t+{{\Delta }}t}-{{{{{{{{\boldsymbol{x}}}}}}}}}_{t}).$$
(17)

Note that their dependence on the realization x( ⋅ ) is omitted in this notation for simplicity.

Specifically, we model the coefficient field d(x, t∣θ) by a feedforward neural network, and conduct the stochastic gradient ascent using an ensemble of single transitions extracted from 104 or 105 trajectories (see Supplementary Note 1 for the details of the implementation) with Δt = 10−2s and τobs = 1s. We note that, in recent experiments with colloidal systems, a few thousand of realizations of the trajectories have been realized with sampling intervals as small as Δt = 10−6s62, and trajectory lengths as long as many tens of seconds60,61.

A feedforward neural network is adopted because it is suitable for expressing the non-trivial functional form of the thermodynamic force F(x, t)30,63, and for continuous interpolation of discrete transition data64. In Fig. 1b, the entropy production is estimated along a single trajectory. We can confirm the good agreement with the analytical value. In Fig. 1c, d, the entropy production rate is estimated using 104 and 105 trajectories. In both cases, the simple dual representation is used to train the model function on half the number of trajectories. On the other half, we use both the simple dual representation as well as the variance-based estimator in Eq. (14) for the estimation, in order to compare their relative merits. We see, quite surprisingly, that the variance-based estimator performs better than the simple dual representation and has much less statistical error. Since the simple dual representation is essentially just a weighted sum of the mean and variance, this implies that the error in it is due to the noise in the mean, as also explained above (and in Supplementary Note 2).

Another advantage of our method is that it also spatially resolves the thermodynamic force F(x, t), which would be hard to compute otherwise. To demonstrate this point, we further analyze a two-dimensional model that has been used to study the adaptive behavior of living systems21,44,65,66. The model consists of the output activity a, the feedback controller m, and the input signal l, which we treat as a deterministic protocol. The dynamics of a and m are described by the following coupled Langevin equations:

$$\dot{a}(t)=-\frac{1}{{\tau }_{a}}\left[a(t)-\bar{a}(m(t),l(t))\right]+\sqrt{2{{{\Delta }}}_{a}}\ {\eta }_{a}(t),\quad$$
(18a)
$$\dot{m}(t)=-\frac{1}{{\tau }_{m}}a(t)+\sqrt{2{{{\Delta }}}_{m}}\ {\eta }_{m}(t),$$
(18b)

where ηa and ηm are independent Gaussian white noises, \(\bar{a}(m(t),l(t))\) is the stationary value of a given the instantaneous value of m and l, and a linear function \(\bar{a}(m(t),l(t))=\alpha m(t)-\beta l(t)\) is adopted in this study.

We consider dynamics after the switching of the input as described in Fig. 2a. For separation of time scales τm ≫ τa, the activity responds to the signal for a while before relaxing to a signal-independent value, which is called adaptation44. Adaptation plays an important role in living systems for maintaining their sensitivity and fitness in time-varying environments. Specifically, this model studies E. coli chemotaxis21,44,65,66 as an example. In this case, the activity regulates the motion of E. coli to move in the direction of a higher concentration of input molecules by sensing the change in the concentration as described in Fig. 2a.

Fig. 2: Estimation in the adaptation model.
figure 2

a Sketch of the model. The line with an arrow represents activation, and the line with a flat end represents inhibition. The average dynamics of the output activity a and the feedback controller m after the switching of the inhibitory input l are plotted. b Estimated entropy production rate. The blue circles are the estimated values of a single trial (using 104 trajectories) using the variance-based estimator (Eq. (14)). The black line is the true entropy production rate. The labels d1, d2, and d3 are the time instances when we also estimate the thermodynamic force as shown in (c). c Analytical solutions for the thermodynamic force at the instances d1, d2, d3, and (d) estimates over 104 trajectories. Here the horizontal axis is the direction of a, the vertical axis is that of m, and an arrow representing the size of 100 is shown at the top of each figure for reference. The brighter the color, the larger the thermodynamic force as shown in the color bar. Note that in this particular case, the thermodynamic force becomes weaker as time evolves, and hence the size of the vectors reduces. The system parameters are set as follows: the time constants τa = 0.02, τm = 0.2, the coefficients of the mean activity function α = 2.7, β = 1, the strengths of the white noise Δa = 0.005(t < 0), 0.5(t ≥ 0), Δm = 0.005, and the inhibitory input l(t) = 0(t < 0), 0.01(t ≥ 0), which are taken from realistic parameters of E. coli chemotaxis65,66. The trajectories of length τobs = 0.1 are generated with the time interval Δt = 10−4. The simple dual representation (Eq. (10)) is used for training the model function.

Full size image

In this setup, the system is initially in a non-equilibrium stationary state (for t < 0), and the signal change at t = 0 drives the system to a different non-equilibrium stationary state. We show the results of the estimation of the entropy production rate and the thermodynamic force in Fig. 2b, c, respectively. Because of the perturbation at t = 0, the non-equilibrium properties change sharply at the beginning. Nonetheless, the model function d(x, t∣θ*) estimates the thermodynamic force well for the whole time interval (Fig. 2c), and thus the entropy production rate as well (Fig. 2b). In particular, we plot the result of a single trial in Fig. 2b, which means that the statistical error is negligible with only 104 trajectories. We note that the entropy production rate is orders of magnitude higher than that of the breathing parabola model. The results of Figs. 1 and 2 demonstrate the effectiveness of our method in estimating a wide range of entropy production values accurately. In the numerical experiments, we have used Δt = 10−4s. We note that sampling resolutions in the range Δt = 10−6s to 10−3s have been shown to be feasible in realistic biological experiments67. We also note that an order of 103 realizations are typical in DNA pulling experiments68.

The thermodynamic force in Fig. 2c has information about the spatial trend of the dynamics as well as the associated dissipation since it is proportional to the mean local velocity F(x, t) ∝ j(x, t)/p(x, t) when the diffusion constant is homogeneous in space. At the beginning of the dynamics (t = 0), the state of the system tends to expand outside, reflecting the sudden increase of the noise intensity Δa. Then, the stationary current around the distribution gradually emerges as the system relaxes to the new stationary state. Interestingly, the thermodynamic force aligns along the m-axis at t = 0.01, and thus the dynamics of a becomes dissipationless. The dissipation associated with the jumps of a tends to be small for the whole time interval, which might have some biological implications as discussed in Refs. 21,66.

So far, we have shown that our inference scheme estimates the entropy production very well in ideal data sets. Next, we demonstrate the practical effectiveness of our algorithm by considering the dependence of the inference scheme on (i) the sampling interval, (ii) the number of trajectories, (iii) measurement noise, and (iv) time-synchronization error. The analysis is carried out in the adaptation model, for times t = 0 and t = 0.009, at which the degrees of non-stationarity are different. The results are summarized in Fig. 3. In most of the cases, we find that the estimation error defined by \(\left|\widehat{\sigma }(t)-\sigma (t)\right|/\sigma (t)\) is higher at t = 0 when the system is highly non-stationary.

In Fig. 3a, b, we demonstrate the effect of the sampling interval Δt on the estimation. For both the t values, we find that the estimation error does not significantly depend on the sampling interval Δt in the range 10−5 to 10−3, which demonstrates the robustness of our method against Δt.

In Fig. 3c, d, we consider the dependence of the estimated entropy production rate on N—the number of trajectories used for the estimation. We find that roughly 103 trajectories are required to get an estimate that is within 0.25 error of the true value for t = 0.009. On the other hand, we need at least 104 trajectories at t = 0 to get an estimate within the same accuracy. This is because the system is highly non-stationary at t = 0 and thus the benefit of the continuous-time inference decreases.

Fig. 3: Estimation with imperfect data in the adaptation model.
figure 3

Four variations from ideal data are considered: (a)(b) with different sampling intervals Δt, (c)(d) with a different number of trajectories N, (e)(f) with the measurement noise (Eq. (19)), and (g)(h) with the synchronization error (Eq. (20)). (b)(d)(f)(h) are the error analysis of (a)(c)(e)(g) between the estimated and the true entropy production rate (\(:= | \widehat{\sigma }(t)-\sigma (t)| /\sigma (t)\)) at two time instances t = 0 and 0.009. The strength of the measurement noise Λ is shown in units of Λ0, the standard deviation of m in the stationary state at t > 0. The strength of the synchronization error Π is shown in units of Π0, the approximate time instance when the entropy production rate becomes half of its initial value. The black line is the true entropy production rate as used in Fig. 2. a, b The estimation is robust against the choice of the sampling interval. c, d The number of trajectories required for the convergence is large near the initial highly non-stationary time. e, f As for the strength of the measurement noise Λ increases, the estimate reduces because of the effective increase of the diffusion matrix. A larger time interval as well as correcting the bias (via Eq. (S4) of Supplementary Note 1) substantially mitigate this effect. g, h The estimate becomes an averaged value in the time direction. In contrast to (e)(f), the time interval dependence is small. For (a)–(h), the simple dual representation (Eq. (10)) is used for training the model function, and the variance-based estimator (Eq. (14)) is used for the estimation. The mean of ten independent trials are plotted, and the error bars correspond to the standard deviation divided by \(\sqrt{10}\). The system parameters are the same as those in Fig. 2 except τobs = 0.01.

Full size image

In Fig. 3e, f, the effect of measurement noise is studied. Here, the measurement noise is added to trajectory data as follows:

$${{{{{{{{\boldsymbol{y}}}}}}}}}_{j{{\Delta }}t}={{{{{{{{\boldsymbol{x}}}}}}}}}_{j{{\Delta }}t}+\sqrt{{{\Lambda }}}{{{{{{{\boldsymbol{{\eta }}}}}}}}}^{\,{j}},$$
(19)

where Λ is the strength of the noise, and η is a Gaussian white noise satisfying \(\langle {\eta }_{a}^{i}{\eta }_{b}^{j} \rangle ={\delta }_{a,b}{\delta }_{i,j}\). The strength Λ is compared to Λ0 = 0.03 which is around the standard deviation of the variable m in the stationary state at t > 0. We find that the estimate becomes lower in value as the strength Λ increases, while a larger time interval for the generalized current can mitigate this effect. This result can be explained by the fact that the measurement noise effectively increases the diffusion matrix, and its effect becomes small as Δt increases since the Langevin noise scales as \(\propto \sqrt{{{\Delta }}t}\) while the contribution from the measurement noise is independent of Δt. Since the bias in \(\widehat{{{{{{{{\rm{Var}}}}}}}}({J}_{{{{{{{{\boldsymbol{d}}}}}}}}})}\) is the major source of the estimation error, we expect that the use of a bias-corrected estimator31,69 will reduce this error. Indeed, we do find that the bias-corrected estimator, star symbols in Fig. 3e, f, significantly reduces the estimation error (see Supplementary Note 1 for the details).

Finally, in Fig. 3g, h, the effect of synchronization error is studied. We introduce the synchronization error by starting the sampling of each trajectory at \(\tilde{t}\) and regarding the sampled trajectories as the states at t = 0, Δt, 2Δt, . . . (actual time series is \(t=\tilde{t},\tilde{t}+{{\Delta }}t,...\)). Here, \(\tilde{t}\) is a stochastic variable defined by

$$\tilde{t}=\left\lfloor \frac{{{{{{{{\rm{uni}}}}}}}}(0,{{\Pi }})}{{{\Delta }}t^{\prime} }\right\rfloor {{\Delta }}t^{\prime} ,$$
(20)

where uni(0, Π) returns the value x uniformly randomly from 0 < x < Π, the brackets are the floor function, and \({{\Delta }}t^{\prime} =1{0}^{-4}\) is used independent of Δt. The strength Π is compared to Π0 which approximately satisfies σ(Π0) ≈ σ(0)/2. We find that the estimate becomes an averaged value in the time direction, and the time interval dependence is small in this case.

In conclusion, we find that our inference scheme is robust to deviations from an ideal dataset for experimentally feasible parameter values and even steep rates of change of the entropy production over short-time intervals.

Conclusion

The main contribution of this work is the insight that variational schemes can be used to estimate the exact entropy production rate of a non-stationary system under arbitrary conditions, given the constraints of Markovianity. The different variational representations of the entropy production rate: σNEEP, σSimple, and σTUR, as well as their close relation to each other, are clarified in terms of the range of applicability, the optimal coefficient field, and the tightness of the bound in each case, as summarized in Table 1.

Our second main contribution is the algorithm we develop to implement the variational schemes, by means of continuous-time inference, namely using the constraint that d* has to be continuous in time, to infer it in one shot for the full-time range of interest. In addition, we find that the variance-based estimator of the entropy production rate, performs significantly better than other estimators, in the case when our algorithm is optimized to take full advantage of the continuous-time inference. We expect that this property will be of practical use in estimating entropy production for non-stationary systems. The continuous-time inference is enabled by the representation ability of the neural network and can be implemented without any prior assumptions on the functional form of the thermodynamic force F(x, t). Our work shows that the neural network can effectively learn the field even if it is time-dependent, thus opening up possibilities for future applications to non-stationary systems.

Our studies regarding the practical effectiveness of our scheme when applied to data that might conceivably contain one of several sources of noise, indicate that these tools could also be applied to the study of biological19 or active matter systems70. It will also be interesting to test whether these results can be used to infer new information from existing empirical data from molecular motors such as kinesin71 or F1-ATPase72,73. The thermodynamics of cooling or warming up in classical systems74 or the study of quantum systems being monitored by a sequence of measurements75,76,77,78 are other promising areas to which these results can be applied.