Introduction

Flocking is a fascinating self-organized phenomenon observed in a large number of artificial and biological systems1,2, including bacterial swarms3,4,5,6, fish schools7, and sheep herds8, among many other examples. The large-scale properties of these active systems crucially depend on the type of interaction neighborhood of the moving agents. Two fundamentally different types of interaction neighborhood have been explored, the so-called metric9 and topological ones10.

In metric models, the neighborhood of a particle is defined via the Euclidean distance between the focal and the neighboring particles, and the number of neighbors of the focal particle scales with the local particle density. As a result of the competition between velocity alignment among neighbors and noise-induced decoherence, metric flocking models undergo spontaneous symmetry breaking2. In ideally homogeneous media, the order that emerges in these non-equilibrium systems in two dimensions is long-ranged (LRO)11,12, giant density fluctuations12,13 are observed, and the phase transition is characterized by the presence of high-order, high-density bands that move across the system14,15,16,17,18,19,20. The presence of spatial heterogeneities or quenched disorder (e.g., obstacles, inhomogeneous substrates, etc.), ubiquitous in all experimental and real-world active systems21, dramatically affects the large-scale properties of metric flocking models. In scalar active matter, it was found that obstacles can lead to jamming, frozen states, and moving chains22,23,24,25. For vectorial active matter in the presence of quenched disorder, it was shown first numerically26 and later analytically27 that order becomes quasi-long-ranged (QLRO). It was also found, using a minimal model, there exists an optimal noise that maximizes collective motion26, a result later confirmed in more realistic simulations28. Furthermore, it was also predicted that spontaneous particle trapping leading to anomalous transport can occur29, a prediction in line with recent findings in bacteria30. In addition, it was also shown the existence of multiple attractors for flocks flying through the same realization of quenched disorder, meaning that the fate and history of the flock are strongly dependent on the initial condition31. Finally, it was found in models32 and experiments33, that above a given density of spatial heterogeneities, polar bands vanish.

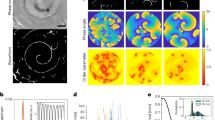
While metric flocking models have been successful in reproducing several real active systems, it has been suggested that animals interact with a specific number of neighbors, regardless of local density, and thus independently of the relative Euclidean distance between the individuals10. The large-scale properties of topological flocking models are believed to be fundamentally different from the ones of the metric counterparts. In particular, the phase diagram of these systems, so far only studied in homogeneous media, does not seem to possess a coexistence region characterized by the presence of polar, traveling bands34,35,36; Fig. 1a, d. The absence of traveling bands has been attributed to an apparent lack of a density-order coupling. On the other hand, the impact of quenched disorder on the active matter with topological interactions has, so far, not been addressed.

Fig. 1: The role of heterogeneity in flocking with topological interactions.
figure 1

Panels a–c corresponds to k-nearest neighbors interaction (kNN, k = 6 where k is the number of neighboring objects), and panels d–f are for Voronoi interaction. Snapshots indicate macroscopic configurations, a, d in obstacle-free environments, where obstacle density ρo = 0, and b, e in complex environments, with obstacle density ρo = 0.051. Black and red dots represent particles and obstacles, respectively. The insets in b, e show 1D band profiles, that is 1D particle density ρL along the moving direction. c, f Local order (rℓ) vs local density (ρℓ) measured in small cells of size l = 14 in a simulation box with linear size 140 corresponding to the systems in previous panels (see “Methods” for details). Black scatters are for homogeneous, and red scatters are for heterogeneous environments. Noise intensity is fixed at η = 0.65 here.

Full size image

Here, we address this open question in active matter theory by studying how the quenched disorder affects the emergent properties of topological flocking models using k-nearest neighbors (kNN) and Voronoi tessellation37. We find that topological models differ fundamentally from their metric counterparts by exhibiting long-range order even in the presence of heterogeneities. Furthermore, we observe that in topological models, spatial heterogeneities counter-intuitively facilitate the emergence of traveling, polar bands (Fig. 1b, e; Supplementary Movies 1 and  2), while such elongated structures are believed not to be present in homogeneous media34,38. Finally, we argue that band formation is related to the emergence of an effective coupling between local density and local order (Fig. 1c, f) due to local rewiring of the interaction network, which is strongly enhanced by the presence of spatial heterogeneities.

Our study provides a comprehensive characterization of the large-scale properties of topological flocking models in heterogeneous environments. The results reported here, together with those by Martin et al.38, strongly suggest that the established knowledge on topological flocking models needs to be fundamentally revised. Specifically, our analysis extends our understanding of topological interactions in active matter systems by showing that topological flocking models in complex environments behave as metric ones in homogeneous media.

Results

Model

We consider active particles moving at constant speed v0 in a two-dimensional, heterogeneous environment with periodic boundary conditions. The heterogeneous environment is modeled by a random distribution of “obstacles”, which we also will refer to as quenched disorder or spatial heterogeneities. Each active particle interacts with its topological neighborhood (TN), which defines the particle’s local environment. We use two definitions of TN: (i) the first k-nearest neighbor (kNN) objects, and (ii) all objects in the first shell by performing a Voronoi tessellation. Note that neighboring objects include other active particles, as well as obstacles. The behavior of particles is different for TN objects corresponding to active particles and obstacles: particles align their velocity to that of neighboring active particles and move away from obstacles. The equations of motion of i-th particle are given by:

$${\dot{{{{{{{{\bf{x}}}}}}}}}}_{i}={v}_{0}{{{{{{{\bf{V}}}}}}}}({\theta }_{i})$$
(1)
$$\dot{{\theta }_{i}}=\ {g}_{i}({n}_{o,i})\left[\frac{\gamma }{{n}_{b,i}}\mathop{\sum}\limits_{j\in {{{{{{{\rm{TN}}}_a}}}}}}\sin ({\theta }_{j}-{\theta }_{i})\right]+\frac{\gamma }{{n}_{o,i}}\mathop{\sum}\limits_{s\in {{{{{{{\rm{TN}}}_o}}}}}}\sin ({\alpha }_{s,i}-{\theta }_{i})+\eta {\xi }_{i}(t)$$
(2)

where dots on the left-hand side denote temporal derivatives, xi is the position of the particle, and θi encodes the moving direction of the particle given by \({{{{{{{\bf{V}}}}}}}}({\theta }_{i})=(\cos ({\theta }_{i}),\sin ({\theta }_{i}))\). The first term in Eq. (2) describes the alignment of the particle with TN active particles (subset TNa), while the second term describes repulsion from TN obstacles (subset TNo). The symbol TN denotes the set of topological neighbors of particle i, including nb,i active particles and no,i obstacles. The position of TN obstacles is given by ys, and αs,i denotes the angle, in polar coordinates, of the vector xi − ys. Note that “obstacles” are in fact areas that the active particles avoid by turning away from their center (ys), which can be viewed as a soft-core repulsive interaction. Finally, γ is a constant and ξi is a delta-correlated, dynamic noise such that 〈ξi(t)〉 = 0 and \(\langle {\xi }_{i}(t){\xi }_{j}(t^{\prime} )\rangle ={\delta }_{ij}\delta (t-t^{\prime} )\); η is a constant that denotes the strength of the dynamic noise. We studied two options for gi(no,i) that lead qualitatively to the same results: (a) gi(no,i) = 1 for all values of no,i, and (b) gi(no,i) = 1 − Θ[no,i] with Θ[no,i] = 1 if no,i > 0. The latter option of gi(no,i) ensures that in the presence of obstacles, the active particle gives priority to obstacles, and move away from them, ignoring other active particles. Since results are easier to interpret with this rule, and are qualitatively the same as those obtained with gi(no,i) = 1, we illustrate the system behavior using the obstacle priority rule; results for gi(no,i) = 1 can be found in Supplementary Fig. S1. In the following, we fix γ = 1, v0 = 1, dt = 0.1, and particle density ρb = Nb/L2 = 1, with Nb the number of active particles in the simulation box of linear size L (see “Methods” for further details).

Note, that we have studied the dynamics of the above model recently also in the context of collective information processing37.

Dynamic noise vs. quenched disorder

The system considered here contains two sources of fluctuation that promote misalignment among the active particles: the dynamic noise and the quenched disorder (i.e., the obstacle field). For vanishing dynamic noise—i.e., in the limit of “cold” active matter—the initial condition and specific distribution of obstacles determine the temporal evolution of the flock, implying that the system is not ergodic31. By including a non-vanishing dynamic noise, the system remains strictly speaking non-ergodic; however, time average quantities over long time-intervals can become independent of the initial condition. Furthermore, we can expect that quenched disorder realizations sharing the same statistical properties—e.g., same density of randomly distributed obstacles—lead to similar time average quantities, as occurs for flocking models with metric interactions26.

To disentangle the level of fluctuation resulting from dynamic noise and quenched disorder, we compare the polar order parameter—defined as \(r=\langle r(t)\rangle =\left\langle | \frac{1}{{N}_{b}}{\sum }_{i}\exp ({{{{{\mathrm{i}}}}}}{\theta }_{i})| \right\rangle\) —computed over different realizations of statistically identical disorders; Fig. 2 (see Supplementary Fig. S2 for the corresponding plots of kNN, k = 6). Note that the standard error of the mean, r, over disorder realizations (red vertical lines), is either smaller than or of the same order of the variance of the polar order r(t) over time for a single disorder realization (black curves). This strongly suggests that the large-scale properties of the system are highly similar among disorder realizations that share the same statistical properties. Finally, it is worth mentioning that for a given disorder realization in a finite system, though order can emerge in a large number of directions, not all of them exhibit the same probability.

Fig. 2: Dynamical noise vs quenched disorder.
figure 2

Panels a–c: Black curves correspond to probability density functions of polar order r(t) obtained from stationary regime of 40 simulations with Voronoi interaction and different obstacle configurations, at obstacle density ρo = 0.15 and noise intensity η = 0.05, 0.20, and 0.45 from left to right respectively. Red vertical lines correspond to the mean (time-averaged) polarization of each of the 40 distributions. Panels d–f: Probability density function of the mean polarization values.

Full size image

Optimal noise and long-range order

As shown in Fig. 3a–c, the polar order parameter is a monotonically decreasing function of the noise strength η in homogeneous environments with vanishing obstacle density ρo = 0, whereby ρo = No/L2 and No is the number of obstacles in the system. One of the most remarkable features of metric flocking models in complex environments, i.e., for ρo > 0, is the non-monotonic functional form of the curve r vs. η that puts in evidence the presence of an optimal noise that maximizes collective motion26. This optimal noise is absent in topological flocking models with kNN interaction: the curve r vs. η decreases monotonically with η for all tested values of ρo, as occurs in homogeneous media, see Fig. 3b (see Supplementary Fig. S3 for the transition plots of other k values). The situation for Voronoi interaction is rather different. By increasing obstacle density ρo from zero, a weak maximum appears in the curve r vs. η, see Fig. 3c, which tends to become weaker by further increasing ρo. One possible explanation for the lower order observed at low noise values is the formation of moving, high-density clusters that are only weakly interconnected among them, see Fig. 3d–f and Supplementary Movie 3. As observed for active particles with metric interactions in heterogeneous media26,32, we also find for Voronoi interaction, that small, yet finite values of dynamical noise facilitate exchange of directional information between clusters. At the optimal noise value, the different clusters merge into a band-like structure and the global orientational order becomes maximal. A further increase of dynamical noise leads then to a monotonous decrease in order. In short, the existence of an optimal noise in topological flocking models seems to be model-dependent.

Fig. 3: Disorder to order transition.
figure 3

Polar order parameter r versus noise intensity η at different obstacle densities ρo for different types of interaction neighborhoods, metric (a), k-nearest neighbors (kNN, k = 6 where k is the number of neighboring objects) (b), and Voronoi (c). d The snapshot shows a typical configuration forming in a system with Voronoi interaction in heterogeneous environments at low noise values, here η = 0.05, and ρo = 0.051. Black and red dots represent particles and obstacles respectively. The arrow shows the instantaneous polarization of the system. e, f Show magnification of the region displayed in (d). In e, black arrows show the particles' instantaneous moving direction. In f the underlying (undirected) Voronoi interaction network is depicted. A link exists between two particles, if they are neighbors in the Voronoi tessellation, and if at least one of them does not have an obstacle in its neighborhood. The green circles point out clusters that are connected by long links, i.e., long-distance interactions. Error bars represent the standard deviation of the polar order parameter over different realizations of the obstacle field (see “Methods”). Note that error bars are often comparable or smaller than the symbol size.

Full size image

A fundamental difference between topological and metric flocking models in complex environments is observed at the level of the emergent order. Metric flocking models in homogeneous media display LRO, while in heterogeneous media, the order was shown, first numerically26 and later by an RG argument27, to become QLRO: the polar order parameter r decays algebraically with system size. On the other hand, topological models in homogeneous media and non-vanishing ρb = Nb/L2, with Nb being the number of active particles, also exhibit LRO34,35. By keeping ρb and ρo constant, while increasing Nb and No, we provide solid numerical evidence indicating that the polar order parameter r converges towards a constant value in the thermodynamic limit for both kNN and Voronoi neighbors at low and high obstacle densities. Specifically, \({{{{{{{\mathrm{lim}}}}}}}\,}_{1/{N}_{b}\to 0}r\to {r}_{\infty }\), with r∞ a non-vanishing constant; Fig. 4.

Fig. 4: Probing the existence of long-range order.
figure 4

Polar order parameter r vs inverse system size 1/Nb at different noise values (η) and obstacle densities (ρo). Panels a, c correspond to k-nearest neighbors interaction (kNN, k = 6 where k is the number of neighboring objects), and panels b, d are for Voronoi interaction. a, b ρo = 0.051 and c, d ρo = 0.153. Error bars represent the standard deviation of the polar order parameter over different realizations of the obstacle field (see “Methods”). Note that error bars are often comparable or smaller than the symbol size.

Full size image

This result can also be obtained by studying \(\langle \bar{{{{{{{{\bf{V}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\bar{{{{{{{{\bf{V}}}}}}}}}({{{{{{{\bf{0}}}}}}}})\rangle\), where \(\bar{{{{{{{{\bf{V}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\) refers to the local, average velocity of active particles in position r, that as expected for LRO converges to a non-zero value for ∣r∣ → ∞, see Supplementary Fig. S4. In addition, we have also confirmed the robustness of the observed LRO with respect to variation in the particle density ρb by simulating systems with a larger and smaller density, ρb = 1.5 and ρb = 0.5 respectively (see Supplementary Fig. S5).

In short, topological flocking models in heterogeneous media exhibit LRO, in contrast to the QLRO reported for the metric counterpart. We note that as discussed further below, we observe the formation of large-scale bands for a wide range of parameters, in particular for the kNN model with k = 6. Thus the corresponding LRO results are obtained in the presence of such emergent spatial structures.

Traveling polar bands

In metric flocking models in homogeneous media, the emergence of polar bands has been explained as the result of a coupling between local polar order rℓ and local density ρℓ17 (see “Methods” for details regarding calculation of rℓ and ρℓ). On the other hand, topological flocking models have been introduced as active models that lead to large-scale collective motion independently of the local density of the active particles10. In short, it has been assumed that in topological flocking models the above-mentioned order-density coupling is not present. Thus, traveling polar bands are not expected to emerge, as illustrated in Fig. 1a, d for Voronoi and kNN neighbors in homogeneous media. Figure 1b, e and Figs. 5a, 6a show that, counter-intuitively, by introducing inhomogeneities in the system, i.e., for ρo > 0, traveling polar bands spontaneously emerge in topological flocking models across a wide range of parameters (see also Supplementary Movies 1 and 2). Moreover, for ρo > 0 an effective order-density coupling, not observed for ρo = 0, is present using both, Voronoi and kNN neighbors (Fig. 1c, f). To quantify the emergence of traveling, polar bands we introduced a density modulation parameter β, defined via the amplitude of the largest Fourier mode with finite wave number q > 0 of the Fourier-transformed coarse-grained density field (see “Methods” for details). Figure 5b–e indicates β at different noise values η and obstacle densities ρo for k = 1 and k = 6. For k = 1, bands are observed only near transition point (orange and red regions). By increasing k—e.g., to k = 6—and ρo, bands are observed for all η values such that η < ηc,H, where ηc,H is the critical value in homogeneous media (Fig. 5). We have confirmed that band structures emerge also for larger k (e.g., k = 12) over a wide range of parameters, in particular, different noise intensities also away from the order-disorder transition (see Supplementary Fig. S6).

Fig. 5: Emergent bands in k-nearest neighbors interaction (kNN).
figure 5

a Typical macroscopic configurations observed in a system with k-nearest neighbor interaction (kNN, k = 6, where k is the number of neighboring objects), for different obstacle densities ρo, and noise intensities η. Black dots are particles and red dots are obstacles. In obstacle-free environments (ρo = 0), we observe rather homogeneous structures with no bands. As we introduce obstacles, band-like structures emerge; at a fixed noise, by increasing obstacle density, bands become sharper. For a fixed obstacle density, the sharpest bands are observed at low noise values. Snapshots specified by I, II, and III have been used to calculate 1D band profiles in panel (c). b Density modulation parameter β in different regions of phase space specified with obstacle density ρo and noise intensity η corresponding to the system in panel (a). 1D band profiles related to I, II, and III are shown in (c). c 1D band profiles—1D particle density ρL along the moving direction L (x or y)—corresponding to the specified regions of panels (a, b) (regions I, II, and III). d β vs obstacle density ρo, showing the promoting effect of obstacles in band formation, corresponding to η = 0.25 in panel (b). e Density modulation parameter β for k = 1.

Full size image
Fig. 6: Bands in Voronoi interaction.
figure 6

a Typical macroscopic configurations observed in a system with Voronoi interaction, for different obstacle densities ρo, and noise intensities η. Black dots are particles and red dots are obstacles. In obstacle-free environments (ρo = 0), we observe rather homogeneous structures with no density segregation in the form of cluster or band. In heterogeneous environments, we observe cluster-like structures at low noise values, here η = 0.05, these clusters connect together to form bands at noise around η = 0.20 and lead to a maximum in polar order parameter (see Fig. 3c). Bands continue to form at higher noise values. b Density modulation parameter β in different regions of phase space specified with obstacle density ρo and noise intensity η corresponding to the system in panel (a). It should be noted that since macroscopic structures for Voronoi interaction are different from those with k-nearest neighbors interaction (kNN, where k is the number of neighboring objects), with clusters at low noise values and bands at higher noise values, the same color (i.e., reddish regions) may refer to different types of structures when comparing to kNN interaction, and even for Voronoi when comparing high and low noise values.

Full size image

A core finding is that for fixed values of η and k, bands become more pronounced as the obstacle density ρo is increased; Fig. 5 (and Fig. 6 for Voronoi interaction). This means that counter-intuitively the spatial heterogeneities promote band formation, while in metric models they hinder the formation of bands26. It is worth clarifying that this does not mean that spatial heterogeneities promote polar order, which decreases as ρo increases. However, the presence of obstacles induces, as explained below, a coupling between local density and local (polar) order that leads to band formation. An important observation is that the speed of bands is independent of ρo—i.e., of quenched disorder—and set by the amplitude η of dynamic noise (see Supplementary Fig. S7a−d). As the density ρo is increased, the number of active particles traveling in the bands diminishes, the disorder gas density increases, and as a result of this, the global polarization of the system decreases. One important lesson to draw is that it is not possible to reduce the impact of spatial heterogeneities to a re-normalized dynamic noise, since this would imply that the band speed depends on ρo, which, we show, it does not.

Discussion

How can spatial heterogeneities promote band formation? In the following, we argue that (local) rewiring of the underlying dynamical network leads to an effective density-order coupling. Our argument is based on the following observations: (i) local (orientational) order is strongly regulated by the level of (local) rewiring facilitating the fast exchange of orientational information between different sets of particles, (ii) obstacles induce local rewiring, and (iii) rewiring is strongly density-dependent, i.e., at high densities, it will occur highly localized in space. This, together with the two previous points results in an emergent coupling between local (particle) density and local order, a necessary condition for band formation.

The first assertion can be shown using a simple model. Assume a finite system of Ns spins that when not connected to each other obey \({\dot{\theta }}_{s}=\eta {\xi }_{s}(t)\). At a rate, ν pick a pair i−j of spins and connect them for a finite time during which \({\dot{\theta }}_{i}=\gamma \sin ({\theta }_{j}-{\theta }_{i})+\eta {\xi }_{i}(t)\) and \({\dot{\theta }}_{j}=\gamma \sin ({\theta }_{i}-{\theta }_{j})+\eta {\xi }_{j}(t)\); for details see “Methods”. In this simple model, order—i.e., \(| {\sum }_{s}\exp ({{{{{\mathrm{i}}}}}}{\theta }_{s})/{N}_{s}|\) —increases with rewiring rate ν (Supplementary Fig. S8a). This non-spatial model serves to prove that local rewiring can promote order.

The next step of the argument is to understand that the spatial motion of agents implies rewiring. This is evident for diffusing spins with metric interactions, where the order is enhanced at larger densities or by using larger diffusion coefficients39. Here, both effects result in a faster exchange of interaction partners. In actual flocking models, however, the situation is more complex since particle velocity is coupled to θi and it is not possible to control the rewiring rate ν—defined as the inverse of the average time an edge survives in the dynamical network—without affecting the dynamics of θi. However, simulations performed with topological flocking models in small systems—Supplementary Fig. S8b and “Methods”—allow us to show that (local) polar order and the rewiring rate ν increase with the density of active particles ρb. Furthermore, in the vicinity of obstacles, active particles are forced to modify their trajectories, which affects the distance to neighboring particles, and leads, in consequence, to rewiring. Figure 7a, d confirms that, as expected, ν increases with the density of obstacles ρo. Here, we note that a finite obstacle density introduces naturally a characteristic maximal metric length scale of rewiring of the order of average obstacle distance \(1/{\sqrt{\rho }}_{o}\).

Fig. 7: Quantifying rewiring and the (local) density-order coupling in the k-nearest neighbor interaction (kNN).
figure 7

The number of neighbors is k = 1 (a–c) and k = 6 (d–f). a, d The rewiring rate ν as a function of obstacle density ρo for different values of dynamical noise. Error bars represent the standard deviation of rewiring over different realizations of the obstacle field. Note that error bars are often comparable or smaller than the symbol size. b, e Local order rℓ versus local particle density ρℓ for different obstacle densities ρo (see “Methods” for details); the corresponding value of mutual information MI(ρℓ, rℓ) is also reported. c, f Mutual information MI(ρℓ, rℓ) versus dynamical noise and obstacle density. The dashed lines indicate the dynamical noise strength η = 0.35 used in (b, e), with points indicating the corresponding obstacle densities.

Full size image

Finally, to quantify the coupling between local density ρℓ and local order parameter rℓ we calculate the mutual information MI(ρℓ, rℓ) as a measure of the non-linear correlation between ρℓ and rℓ, i.e., we quantify how much knowledge we gain on rℓ by knowing ρℓ (see Fig. 7b, c, e, f). It is important to note that rℓ is by definition bounded to values smaller or equal to 1. For certain parameter choices, rℓ saturates to almost 1 for all ρℓ values. This occurs for instance at low dynamic noise and low obstacles densities. In these situations, it is evident that rℓ is independent of ρℓ, and thus MI(ρℓ, rℓ) adopts low values. Note that for rℓ ~ 1 particles are highly aligned and the relative distance between particles remains relatively constant implying a low rewiring rate. On the other hand, in the disordered state, we observe rℓ ≈ 0 for all ρℓ. Overall, in order for rℓ to be dependent on ρℓ, the system cannot be too disordered but also the level of polar order in the system should not be too high. This suggests, as actually observed, that sharper bands are observed at larger obstacle densities, where the level of global order is lower (see Supplementary Fig. S7e). In particular, for a fixed dynamic noise, MI(ρℓ, rℓ) is higher, indicating a stronger correlation between rℓ and ρℓ, for larger obstacle densities ρo, where the rewiring rate ν is also higher; see Fig. 7 and compare band snapshots in Figs. 5 and 6.

An interplay between rℓ and ρℓ mediated by rewiring is arguably also present in spatially homogeneous systems. For fixed dynamic noise, it is expected that ν decreases with k and increases with particle density ρb. Both trends are straightforward to understand under the assumption that the level of positional fluctuations of the particles is set by dynamic noise. For large values of k, positional fluctuations only lead to the replacement of the farthest neighbors, and this implies that most links (those corresponding to closer neighbors) are long-lived. In consequence, the average time an edge survives increases with k, and its inverse, ν, decreases. On the other hand, at high densities the average inter-individual distance between particles is small, and for the same level of positional fluctuations, a higher rewiring rate is expected. Simulations performed in an homogeneous medium, Fig. 8, are consistent with these arguments. In addition, all this suggests that the coupling between rℓ and ρℓ in homogeneous media should be particularly strong for small k values in the vicinity of the onset of order. Figure 8c shows that in an homogeneous medium for k = 1 traveling bands robustly emerge, whereas they become quickly more diffuse with increasing k and at k = 6 are not observable in our simulations anymore (see bottom panels in Fig. 5a). This finding provides additional support for our arguments. At this point, we also would like to point the reader to a recent publication38, which we learnt about at the time of submission, providing an alternative explanation for band formation in homogeneous media of flocking models with topological interaction. We note that the different mechanisms are not mutually exclusive in facilitating band formation in active matter with topological interactions.

Fig. 8: Observed bands for the k-nearest neighbor interaction (kNN) in homogeneous environments.
figure 8

k is the number of neighbors and the density of obstacles is fixed at ρo = 0. a Rewiring ν versus k for a system with Nb = 625 particles (particle density ρb = 1.0), interacting with kNN. b Rewiring ν measured for the system with Nb = 625 at different particle densities ρb by varying box size L (k = 6). c) Snapshot showing band formation for kNN interaction with k = 1. The black dots represent particles, and the green arrow shows the moving direction of the band. Noise intensity is η = 0.55 for all the panels.

Full size image

Conclusions

We performed a comprehensive study of flocking models with topological interactions in heterogeneous environments. We investigated two different types of topological interactions, kNN and Voronoi, which are the two most studied active topological models in the literature10,34,35,36,38. Similarly to what occurs in an equilibrium system, where only few macroscopic details affect the emergent macroscopic behavior, here we found that the large-scale properties of these systems do not depend on the details of the implementation of the model—e.g., on the choice of gi(no,i)—but on the nature of these interactions: i.e., topological (metric-free) interactions of polar symmetry. In that sense, our results are generic and we expect them to apply to other variations of topological interactions, as for example the spatially balanced kNN-model40. The two main results of our work on flocking models with topological interactions in heterogeneous environments are: (1) We found that in sharp contrast to metric models—where we observe quasi long-ranged order (QLRO) in heterogeneous environments—for topological models, according to our numerical study and up to the systems sizes investigated, the order is long-ranged (LRO) in the presence of spatial heterogeneities. (2) We showed that spatial heterogeneities promote the emergence of an effective density-order coupling that allows active particles with topological interactions to form traveling polar bands, which share similar features to the bands observed in metric models. Importantly, bands are observed in parameter ranges in which metric models in homogeneous media do not develop bands. Furthermore, we argued that the counter-intuitive emergence of the density-order coupling for topological interactions is the result of the (local) rewiring of the underlying dynamical networks of active particles induced by the spatial heterogeneities. Finally, we expect that the numerical finding of LRO in heterogeneous media for nonmetric active models—arguably related to the presence of long-ranged connections between distant clusters—will be supported by a RG calculation, as occurred in the past with the observation QLRO in metric models in the presence of quenched disorder26,27.

In summary, our results show that topological flocking models in the presence of spatial heterogeneities—which introduce a characteristic distance (\(1/\sqrt{{\rho }_{o}}\))—behave as metric ones in homogeneous media, an observation that invites to a reconsideration of “metric-free” interactions in active systems.

Methods

Simulation details

The model was implemented in C++ programming language. Stochastic differential equations were solved using the Euler−Maruyama method with an integration time step of dt = 0.1. Topological interactions including kNN and Voronoi implemented using the CGAL computational geometry algorithm library41. For kNN, k-d tree algorithm is used, where in order to account for periodic boundary conditions, the main simulation box has been repeated in different directions. In order to find particles in the first shell of Voronoi neighbors, the dual graph of Voronoi diagram i.e., (periodic implementation of) Delaunay triangulation is used.

All the other calculations and data processing have been done using Python and dependent libraries, in particular Numpy42 and Scipy43. Furthermore, we used NetworkX library44 for network related calculations.

Local density ρ ℓ and local order r ℓ

Density-order coupling plots of Figs. 1 and 7 have been obtained by superimposing the rℓ and ρℓ of 60 snapshots taken from three time windows of simulations. In order to find these local quantities, the simulation box is divided into small cells of linear size ℓ. Accordingly, local density is defined by \(\frac{{n}_{\ell }}{{\ell }^{2}}\), where nℓ is the number of particles in the cell. And, local order is defined by \({r}_{\ell }=| \frac{1}{{n}_{\ell }}{\sum }_{i}\exp ({{{{{\mathrm{i}}}}}}{\theta }_{i})|\), where the summation is over the nℓ particles of the cell. For the simulation box of size 140, we have used a cell size ℓ = 14.

Quantification of bands

1D band profile

In order to obtain 1D band profile, the density field of particles is smoothed using the kernel density estimation algorithm, then integrated over the direction perpendicular to the moving direction. Profiles represented in Fig. 1 are the result of averaging over 200 snapshots taken every 10 time steps.

Band speed

Speed of band is obtained by measuring the displacement of the peak of 1D band profile during a fixed time period.

Bandwidth

Considering 1D band profile, bandwidth is obtained from the difference between two points on the horizontal axis where the height of the profile is equal to a quarter of the maximum value.

Density modulation parameter β

In order to quantify bands occurring in different regions of the parameter space, i.e., different k, ρo, and η, we cannot rely on bandwidth obtained from 1D band profiles. Since, in addition to single bands, we also observe band-like density modulations or multiple bands, some of which are merging and splitting during the course of simulations. Therefore, obtaining a bandwidth, which is representative of configurations of all the time steps, is in general not possible. In order to address this problem, we use the Fourier transformation of the coarse-grained density field and identify the maximal amplitude of the resulting Fourier spectrum for a finite spatial frequency q > 0 (wave number). The density modulation parameter (maximum amplitude), β, is obtained after averaging over the power spectrum of 200 snapshots taken every 10 time steps. Please note that non-zero values of β may also indicate other density modulation besides traveling bands, as for example formation of dense clusters in the Voronoi model for small dynamical noise (see Fig. 6). However, β ≳ 0.5, typically indicates band formation.

Order parameter fluctuations and error bars

There are two kinds of fluctuations that affect the value of the polar order parameter in our system. One stems from different realizations of obstacles in the environment, the so-called quenched disorder, the other is due to fluctuations in particles orientation, that is dynamic noise. The variation of the polar order r(t) due to dynamic noise can be measured through its standard deviation, which will be correlated with the intensity of the dynamical noise. In the context of heterogeneous environments, the error of the (time-averaged) polar order parameter due to different realizations of the quenched disorder is the important quantity. The error bars in Figs. 3 and 4, are calculated from four and five different realizations of random obstacle fields per parameter point, respectively.

From the non-spatial rewiring model to rewiring in small systems

In order to show that rewiring can enhance (orientational) order, we consider a simple non-spatial model. A system of small number, Ns = 10, of spins with initial random orientations is considered. The system is such that at each time step there is only one link connecting two spins, i and j. These two spins align with these rules, \({\dot{\theta }}_{i}=\gamma \sin ({\theta }_{j}-{\theta }_{i})\) and \({\dot{\theta }}_{j}=\gamma \sin ({\theta }_{i}-{\theta }_{j})\), while there is a random contribution ηξs(t) to the orientation of all the spins (s) in the system. The link between i, j remains for m time steps, then another two spins are selected randomly to interact. With this simple model, we show that smaller m, in other words, larger rate ν = 1/tm (tm = dt ⋅ m) of rewiring a single link results in a higher polar order r for the system (see Supplementary Fig. S8a). However, in flocking models, rewiring is associated to the relative motion of the particles, which in turn is related to the level of order. To verify that rewiring is correlated to the local level of order in the flocking model, we performed a series of small size simulations that clearly show such correlation between the rewiring rate ν—which increases with the local density of particles as well as the density of obstacles —and the level of order r; see Supplementary Fig. S8b.